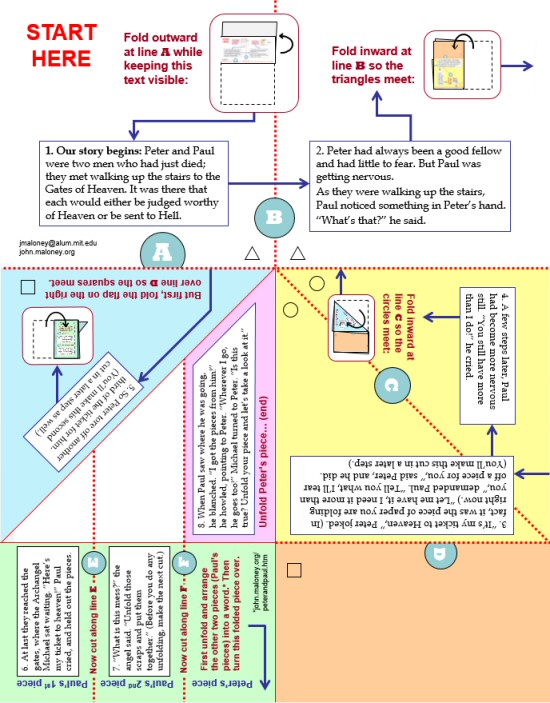
Preface
My version of the Peter and Paul story is here. To my knowledge, it's
the first example of this story appearing directly on the page to be folded.
Now please read on for some background:
Michael Steuben's version
I first encountered the Peter and Paul story in the December 1984 edition of Discover
magazine in the back-page Brain Bogglers section:
At the time, when I pored over this issue, this trick blew my 10-year-old mind. Much later, I contacted
the author, Michael Stueben, who turned out to be a math teacher at Thomas Jefferson High School for Science and Technology, a
few miles from my parents' house in Alexandria, VA. (It's even possible that we
crossed paths at one of the regional math competitions ca. 1990, when I was being
taught by Fr. John Woodward SJ at Gonzaga.)
Mr. Steuben sent a warm response but actually did not recall his article from
1986! That's when you know you're a prolific writer. His version, communicated by email, ran as follows:
“Once upon a time two boys, Peter and Paul, were born in the same small town on the same day. As they grew up they became the best of friends.
Hardly a day went by that they didnít enjoy each otherís company. Eventually they graduated from high school. Peter went one way, Paul went another way, and they never saw each other again.
Peter returned to the town he was born in, began a business, started a family and was known to the townís people as a good Samaritan.
On his death bed he was surrounded by his weeping family, and the last thing Peter said before he died was ‘Gee, I wonder whatever became of Paul.’ And then he died.
Paul turned out to be a terrible person. He cheated, lied, robbed, and spent his last few years rotting in a damp prison cell in some foreign land.
The last words Paul uttered before he died were ‘Gee, I wonder whatever happened to Peter.’ And then he died.
It turns out that these two boys who were born on the same day died on the same day. And the next thing they knew, they were climbing the golden stairs up to Heaven and Judgement day.
[My apologies to the non-Christians in the audience, but this is just a little silly made-up story, like talking about Zeus or Odin.]
Naturally they were delighted to see each other. Peter told Paul all about his wonderful life and Paul just made up a life story to tell Peter.
He was a good liar. But as they were climbing Paul noticed that Peter had this folded piece of paper in his hand. ‘Whatís that?’ asked Paul. ‘Oh, thatís my pass to Heaven,’ replied Peter.
‘Donít you have one?’
‘Oh, I had one, but I dropped it in a cloud, and couldnít find it. But, Iím supposed to go to Heaven, too. Can I have part of yours?,’ asked Paul.
Good Peter who was always obliging said ‘Sure.’ and tore off a third, far from the pointy part, and gave it to Paul.
Eventually, they arrived at the pearly gates of Heaven, and could see the souls streaming in. Paul was getting a little nervous and said.
‘Peter, I noticed that your part of the pass is larger than mine, and that doesnít seem fair.’
‘Oh, you're right,’ replied Peter, and he tore his part of the pass in half, keeping the pointy part, and giving Paul the remainder.
Finally they approached the turn style of Heaven, where Saint Peter was standing and saying ‘Show me your passes! Show me your passes!
Nobody gets into Heaven without a pass, except engineering professors, who have already earned their way into Heaven.’ [A little joke the speaker is allowed to give.]
Paul pushed his way in front of Peter and laid down his two pieces of pass.
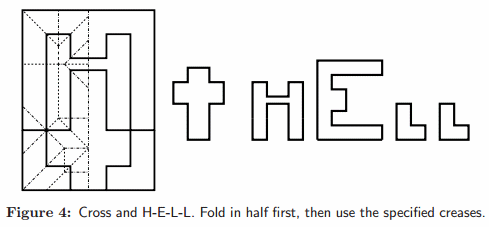
Saint Peter said, ‘Well, what is this? At least unfold and flatten out the pieces so I can see what you have.’ [When the pieces are laid out they spell HELL.]
But Paul was not finished. He said, ‘This isnít my pass. I got it from the guy standing behind me. And If I have to go there, then he must go there too.’
Saint Peter turned to good Peter and said, ‘Where is your pass?’
Good Peter replied, ‘This is all I have left.’
‘Then that is all you need. Unfold it,’ said Saint Peter. [It unfolds into a Christian cross.]”
At this point I should note that Mr. Stueben has had a long and fruitful career
as a teacher and in 1998 published Twenty Years Before the Blackboard: The Lessons and Humor of a Mathematics Teacher with his wife.
It's a fun book—a combination of
mathematical trivia and vignettes of adolescent classroom behavior mixed with comments on
teaching philosophy. It reminds me of one of my favorite
books, Paul Hoffman's biography of Paul Erdős, The Man Who Loved Only Numbers,
which offers a similar blend of mathematical elegance interspersed with warm descriptions of Erdős and his colleagues.
Mr. Stueben continued:
I (current age = 71) was told this story by my father, around 1958, who showed me how to fold the paper to follow the story.
I asked him who showed him. He said his older sister. This must have been around 1932, I am guessing. I eventually found this puzzle
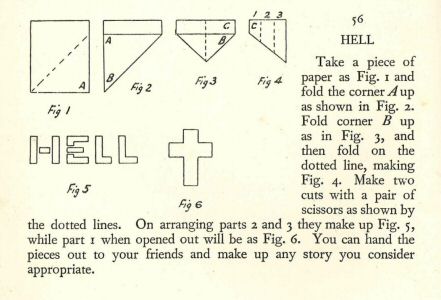
in an old Dover paperback, Easy-to-do Entertainment and Diversions with Coins, Cards, String, Paper, and Matches by R.M. Abraham
(Dover, 1961), page 44, problem 56, which was formerly titled Winter Nights Diversions (published in 1932 or 1933). This book contained
the British term “noughts and crosses,” instead of the American term “tic-tac-toe,” so it probably was not
published in the USA. This and
Abrahamís later Tricks and Amusements (Dover) are some of the more interesting puzzle and playful curiosity books in my collection.
Earlier versions
I bought the book Mr. Stueben mentioned, Winter Night's Entertainment, which was indeed published in Britain in 1932:


And there's an even earlier version in
Modern Mechanics and Inventions from 1929! This one requires a starting aspect ratio of 1:2:
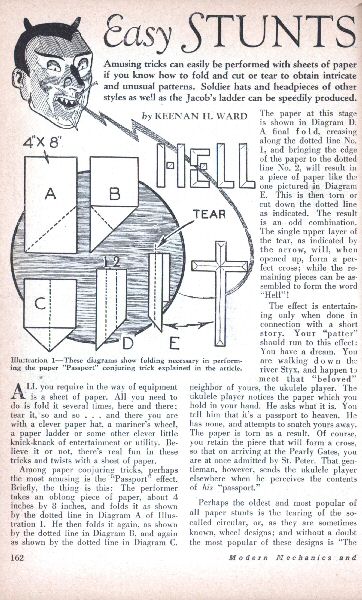
Over the years, this trick has been known
as the ticket-to-heaven, passport-to-heaven, heaven-and-hell, or good-and-evil game.
And as anyone who knows games would expect, polymath Martin Gardner
treaded this path as well.
It's widely noted that Gardner surveyed paper-folding techniques, but
tracking down where he mentioned this particular trick wasn't straightforward. In Mathematical Wizardry for the Gardner,
edited by Pegg et al., David Lister
writes
An article in Scientific American dated June 1960, which is headed “Paperfolding and Papercutting” is mainly about dissections,
but it also touches on papercutting or “kirigami” and it includes the famous dissection puzzle usually known as “Heaven and Hell”.
This is incorrect; I looked up Gardner's June 1960 article in Scientific American, which is actually subtitled “Recreations Involving
Folding and Cutting Sheets of Paper”, and it doesn't include this problem. Wikipedia makes the same error. Presumably they are referring to
the collection of republished Gardner articles (New Mathematical Diversions) with additional content, including the following now-familiar schematic:
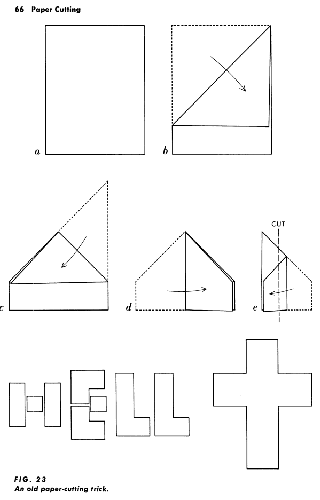
In Gardner's story, the two characters are “contemporary political leaders, one admired, the other hated”. It is suggested that the
admired politician craftily maneuvers the other to take the implicating piece.
I hate to say it, but Gardner either didn't actually try the
steps out himself or got a little sloppy in the description, because in this version, parts from both the left and the right are required to
spell “HELL”. (Stueben's two-cut solution avoids this problem; Paul's two pieces are assembled independently of Peter's piece.)
Modern developments
I'm struck by the great payoff of the exactly appropriate shapes relative to the small number of folds
and cuts. One must conclude that traveling salesmen—or missionaries, or prisoners, or the elderly and infirmed—must
have experimented with countless versions of folded paper tricks that lacked as good a payoff, which
is a little sad. But at least we have this bright standout of all this effort.
In fact, such trial and error may have become largely obsolete. It's now known that any polygon can be produced from a single cut after
suitably folding a single sheet. In “Fold-and-Cut Magic”, Erik D. and Martin L. Demaine published a version that
requires but a single fold and a single cut:
As they describe, “all creases must be folded more or less simultaneously”. Take it from me: this process may be mathematically
expedient, but it isn't fun in practice.
Incorporating the instructions
With the Discover version as my primary guide, I decided to attempt
to present the folding and tearing instructions on the same sheet of paper that would be manipulated; this effort
would require each new instruction to face the viewer after the previous manipulation. Getting all the instructions
on one side of the page required significant changes to the folding steps.
After some experiments with halfway-willing test subjects (relatives and research group
colleagues), it became clear that visually relating the paper's state and orientation over time
would be crucial. I added a large “START HERE” and “Our story begins:” for orientation, but
even more guidance was needed for the participant to confidently make folds
and rotations. Inline sketches of the folding process seemed to be essential, and in investigating ways to portray this information schematically,
I found the following example particularly useful:

Interestingly, the best way to demonstrate how to fold paper correctly is to show
it folded poorly, with several degrees of misalignment!
Along with the schematics (which had to be added in reverse order to get each
sub-schematic to appear correctly!), I also incorporated shapes (e.g., circles and triangles) to be matched:
I then needed to apportion the content across the folds. The arrangement was trivial for
the expositional first half but was trickier when Peter was
actually performing the tearing. Should the participant perform these actions
simultaneously with the story? I couldn't figure out how to synchronize
the action but ultimately selected the crude approach of telling the operator to wait
until instructed:

Even with my best effort, the process gets a little ragged at the end
when one is left holding multiple pieces.
Maybe the need for a human guide is inevitable. The whole point of the puzzle is to achieve the two “reveals”, after all.
Although one of the reveals is just a matter
of unfolding; the other requires assembly. If this second reveal is described
explicitly on the sheet of paper, it becomes trivial and unentertaining; if it's not described,
it understandably mystifies the participant (I've found). I don't know the best solution. The optimal environment may actually be the
original scenario in which, for example, a traveling salesman has the mark follow along with the story to
ultimately sell a set of bibles. Sometimes you just need a guide.
|