Pop quiz
Take two identical systems at equilibrium, one at absolute temperature \(T_1\) (by absolute I mean measured on the Kelvin scale, so instead of 100°C, we’d use 273+100=373 K) and the other at absolute temperature \(T_2\):

Hot (left) and cold (right) systems—otherwise identical—before thermal contact.
If we smush these two systems together into thermal contact (and let’s assume that all material properties are temperature independent), we intuitively figure that when equilibrium is reached, the joint system is at temperature \((T_1+T_2)/2\):

The systems brought together and at thermal equilibrium.
Nature (as idealized in our model) has taken the arithmetic average of the temperatures. OK.
Now, what if we connect the two systems by a perfect heat engine*?
*Examples of a heat engine include the internal combustion engine—the Otto or diesel cycle commonly used in cars and trucks—the steam engine used in old-fashioned locomotives, or other varients such as the Rankine or Stirling cycle. The common element is that we exploit a temperature difference to extract useful energy. For example, we might use heat transfer to expand or boil a working fluid and then use the resulting high pressure to move an object, such as a piston or a turbine. To complete the cycle, we then need to re-compress the fluid. In particular, let’s consider an idealized heat engine, known as a Carnot engine, that operates at perfect efficiency, i.e., one that involves no friction or mechanical inefficiencies or sharp temperature gradients. We could imagine approaching this maximum efficiency through high-quality engineering and by running the engine slowly enough. 
The hot and cold systems connected by a heat engine (shown in silver) that can extract work (indicated by the top arrow) from the temperature difference.
When the heat engine is finished exploiting the temperature difference, the system temperatures have equilized, all such available thermal energy having been extracted:
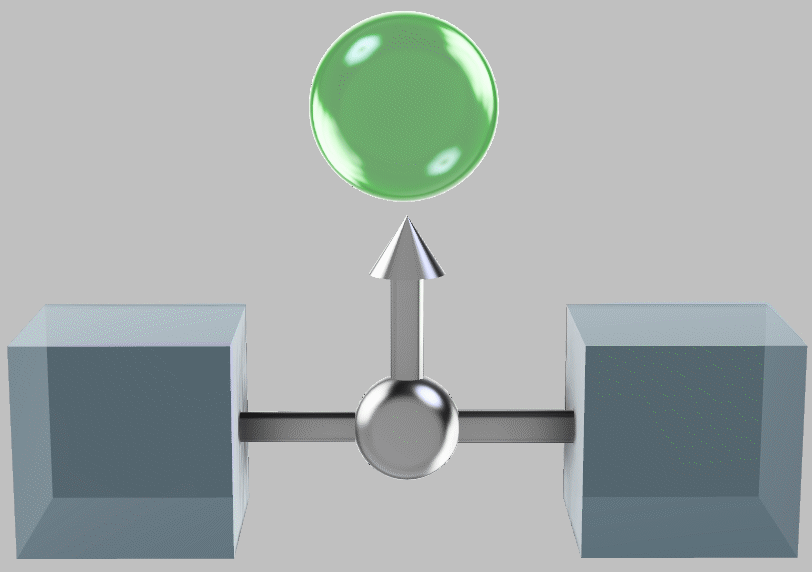
The systems brought together and at thermal equilibrium, having produced a store of energy (green sphere) through work.
What is the temperature of the joint system?
I think the answer (which I derive below, and which I might have given away somewhat by this note’s title) is particularly interesting because it pulls in issues of symmetry in Nature and in mathematical expressions, entropy (that most challenging concept that’s ubiquitous in thermodynamics), the difference between heat and work, and thermodynamic efficiency.
(I don’t mean to suggest at all, though, that this is the only time that Nature takes a square root. Consider, for example, a ball rolling off an incline at a height \(h\); a simple kinematics model tells us that the horizontal deflection of the ball scales with \(\sqrt{h}\). I present the thermodynamics example simply because I’m fascinated by entropy and because a thorough understanding of thermodynamic efficiency is one of the cornerstones of modern civilization.)
A brief review of key thermodynamics concepts involving energy, entropy, heat, and work
First, let’s look at some preliminaries necessary to answer the question—in fact they include the fundamental concepts of thermodynamics:
Energy is conserved. If one system loses energy \(Q\) in contact with another system, then the other system gains energy \(Q\).
Heating a (single-phase) system increases its temperature. Specifically, when we heat an object, the relationship between a small amount of input energy \(q\) and the resulting small increase in temperature \(dT\) is \(q=C\,dT\), where \(C\) is the heat capacity. (Again, we’re assuming temperature-independent \(C\) for this example.)
Entropy is not quite conserved. Specifically, the total entropy never decreases, and entropy is transferred during heat transfer, as discussed in the next point. But in addition, entropy is generated every time energy moves down a gradient (such as a temperature difference).
For these reasons, entropy has sometimes been described as paraconserved: it can’t be destroyed, but it is transferred when one object heats another, and it’s also created whenever any real process occurs, anywhere.
So if we made our gradients very small, we could approach the idealized condition of a reversible process—one in which entropy is perfectly conserved. This is the idealization of the Carnot or perfect heat engine. Now, no real process can ever be perfectly reversible, since Nature requires gradients for spontaneous processes to occur. For simplicity, though, I’ll ignore entropy generation in this note because we can approach reversibility arbitrarily closely in practice.
Heat transfer transfers both energy and entropy. As classified in Section 4 here, for a small amount of heat transfer \(q\) at temperature \(T\), the small amount of entropy transferred is \(dS=q/T\).
But work produced from a closed system transfers no entropy (and reversible work generates no entropy). The lack of entropy transfer when doing work provides one useful distinction between heat and work. Heating a system widens its distribution of energies, whereas doing work on a system increases the energy of all of its constitutive components wholesale. Consider, for example, the difference between increasing the molecular speed of a gas by heating it vs. accelerating its container. In the first case, the distribution of speeds broadens in an undirected manner, and the entropy increases because the broader distribution permits more microstates (i.e., speeds and positions) that are compatible with the system macrostate (i.e., its bulk pressure and temperature). In the second case, the molecules all gain a uniform speed in a certain direction in concert, and the distribution of speeds (ignoring the offset) remains unchanged, as does the entropy, assuming that the acceleration occurres infinitesimally slowly.
Why heat engines need a cold reservoir and why the party boat doesn’t work
This simple framework is tremendously helpful in explaining how heat and work (and heat engines and the resulting output work) operate. Again, work doesn’t transfer entropy, but heat transfer does. Therefore, we can’t simply turn thermal energy into work; we must dump the accompanying entropy somewhere as well. This is why every heat engine requires not just a source of thermal energy (the so-called hot reservoir) but also a sink for entropy (the so-called cold reservoir).

To extract work by cooling the hotter system, we have to dump the associated entropy into the cooler system—there’s nowhere else for it to go.
In the idealized process, when we pull energy \(Q\) from the hot reservoir at temperature \(T_\mathrm{hotter}\), the unavoidable entropy transfer is
\[S=\frac{Q}{T_\mathrm{hotter}}.\]
Now we extract some useful work \(W\) (by boiling water and running a steam turbine, for example), and we dump all that entropy into the low-temperature reservoir at temperature \(T_\mathrm{cooler}\) (using a nearby cool river to condense the steam, for example):
\[S=\frac{Q-W}{T_\mathrm{cooler}}.\]
The energy balance works out:
\[\mathrm{Heat\;leaving\;system\;1}-\mathrm{Extracted\;work}=\mathrm{Energy\;remaining\;to\;heat\;system\;2};\]
\[Q−W=(Q−W).\]
The entropy balance works out:
\[\frac{Q}{T_\mathrm{hotter}}=\frac{Q-W}{T_\mathrm{cooler}}.\]
The efficiency is
\[\frac{W}{E}=1−\frac{T_\mathrm{cooler}}{T_\mathrm{hotter}}.\]
And the lower the temperature of the cold reservoir, the more work \(W\) we can pull out while satisfying the two conservation laws.
Prof. Gerd Ceder at MIT has discussed the instructive example of the party boat: Water can provide a tremendous amount of thermal energy (about 4200 J/kg per °C of temperature change). Even better, water is self-circulating, so we might decide to cool seawater and let it recirculate. We would pull out thermal energy from water to make ice for our cocktails and use the extracted energy to cruise around all day:
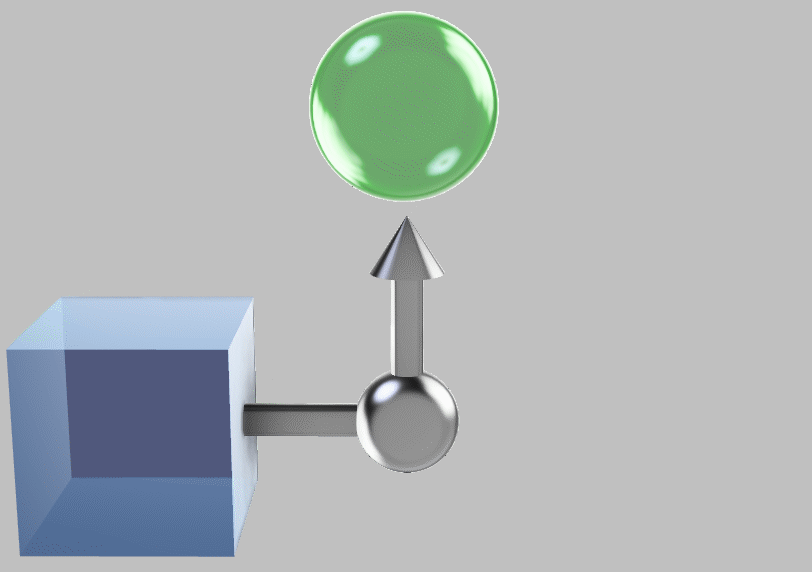
Hypothetical party boat schematized as a heat engine: we remove energy to cool and freeze seawater (blue), producing propulsion to run the boat (green) and ice to cool our drinks. But the scheme doesn’t work because the entropy removed when cooling the seawater has nowhere to go, as the work can carry no entropy.
Unfortunately, the restrictions described above tell us that we can’t perform this extraction: there’s no lower-temperature reservoir to send the entropy to. (Here, I’m assuming that most of the earth and atmosphere available to us is at around the same temperature, say, 10°C.)
There’s a subtle point here: There’s nothing forbidding an expansion step that would completely turn thermal energy into work. In this case, the entropy of the working fluid would stay at least constant because the fluid expands as it cools. The problem comes from compressing the fluid to reattain the original state, which is required for any cyclic engine. During this step, we must dump entropy into a cold reservoir.
Returning to the symmetric systems
With these preliminaries, we’re in good shape to compare the consequences of pushing two systems at different temperatures together vs. exploiting their heat difference with a perfect heat engine.
First, consider the first case of just pushing the systems together:


The hot and cold systems brought together to equilibrate.
We start in state \( 1 \) and end in state \( 2 \), and we’ll turn differential relationships into finite quantities through integration. Consistent with our intuition, the hotter system cools the cooler system. The final temperature \(T_\mathrm{final}=T_\mathrm{hotter,\,state\,2}=T_\mathrm{cooler,\;state\;2}\) is easily calculated by considering the conservation of energy and the heat capacity relations:
\[\mathrm{Energy\;lost\;by\;the\;hotter\;system}=\mathrm{Energy\;gained\;by\;the\;cooler\;system};\]
\[\int_1^2 -E_\mathrm{hotter}=\int_1^2 E_\mathrm{cooler};\]
\[\int_1^2 -C\,dT_\mathrm{hotter}=\int_1^2 C\,dT_\mathrm{cooler};\]
\[C(T_\mathrm{hotter,\;state\;1}-T_\mathrm{hotter,\;state\;2})=C(T_\mathrm{cooler,\;state\;2}-T_\mathrm{cooler,\;state\;1}).\]
Inserting our more familiar variables for systems 1 and 2 and dividing by \(C\), we obtain
\[T_\mathrm{1}-T_\mathrm{final}=T_\mathrm{final}-T_\mathrm{2};\]
\[T_\mathrm{final}=\frac{T_\mathrm{1}+T_\mathrm{2}}{2}.\]
OK, so the ultimate joint-system temperature is \((T_\mathrm{1}+T_\mathrm{2})/2\). This matches our intuition and gets us used to the nomenclature and form of the equations. And this shouldn’t be surprising, right? After all, the systems are identical and we’re combining them in a symmetric way; it’s natural that we should obtain an average—in this case, the arithmetic mean.
Moving on to the symmetric systems connected by a Carnot engine
Now let’s look at the two systems connected by a heat engine to extract energy from their temperature difference, and remember that we’re assuming (for simplicity) that this heat engine is perfect and never generates entropy. Again, such perfection is impossible in reality because all real processes rely on gradients—and is even impractical to implement because the power output of such an engine would drop to zero—but is useful as an idealization in a thought experiment.


The systems connected via a Carnot engine to extract work from the temperature difference.
We can no longer apply the idea of equal energy exchange between the two systems because the heat engine pulls some of that energy out. But we can apply the concept of entropy; the perfect reversibility of the idealized Carnot cycle means that no entropy is generated during heat engine operation. And because reversible work from a closed system carries no entropy, no entropy can leave the two systems. We’re left with the conclusion that any entropy lost by the high-temperature system must be gained by the low-temperature system.
As illustrated by the party boat example, this finding has profound implications for heat engines: Entropy leaves the high-temperature reservoir through heat transfer, but it’s not leaving with the extracted work. You always need a low-temperature reservoir that can receive the entropy, and so a heat engine can operate only between a pair of reservoirs. Importantly, this constraint doesn’t apply to other types of engines (electrochemical engines such as fuel cells, for example), which can turn energy gradients into work with up to 100% efficiency.
So analogous to our first calculation, we have
\[\mathrm{Entropy\;lost\;by\;the\;hotter\;system}=\mathrm{Entropy\;gained\;by\;the\;cooler\;system};\]
\[\int_1^2 -dS_\mathrm{hotter}=\int_1^2 dS_\mathrm{cooler};\]
\[\int_1^2 -\frac{C\,dT_\mathrm{hotter}}{T_\mathrm{hotter}}=\int_1^2 \frac{C\,dT_\mathrm{cooler}}{T_\mathrm{cooler}};\]
\[-C(\ln T_\mathrm{hotter,\;state\;2}-\ln T_\mathrm{hotter,\;state\;1})=C(\ln T_\mathrm{cooler,\;state\;2}-\ln T_\mathrm{cooler,\;state\;1}).\]
Dividing both sides by the heat capacity \(C\), applying the exponential function, and inserting our familiar variables, we obtain
\[\frac{T_\mathrm{1}}{T_\mathrm{final}}=\frac{T_\mathrm{final}}{T_\mathrm{2}};\]
\[T_\mathrm{final}=\sqrt{T_\mathrm{1}T_\mathrm{2}}.\]
The final temperature is thus \(\sqrt{T_1T_2}\), and we find from an energy balance that the extracted energy must be \(2C\left(\frac{T_1+T_2}{2}-\sqrt{T_1T_2}\right)\), which is the difference in energy between the scenarios of just pushing the systems together vs. connecting them via an ideal heat engine.
The resolution
The fact that the final temperature is the geometric mean, \(\sqrt{T_1T_2}\), is elegant. Two equivalent systems are connected in different ways (namely, via direct contact vs. a perfect heat engine), and the result is two distinct types of symmetry: the arithmetic mean \((T_1+T_2)/2\) and the geometric mean \(\sqrt{T_1T_2}\). (This symmetry makes one wonder: Can any other symmetric combinations emerge from related conditions?) Nature takes the square root. And in the process, we review and apply key thermodynamics concepts.
More general cases
What if more than two systems exist? Extending the above calculations to the general case, we find that simply pushing \(N\) systems together produces a final temperature of the arithmetic mean of the original temperatures:
\[T_\mathrm{final}=\sum_{i=1}^N T_i/N.\]
In contrast, applying a heat engine to extract all available thermal energy produces a final temperature of the geometric mean of the original temperatures:
\[T_\mathrm{final}=\left(\prod_{i=1}^N T_i\right)^{1/N}.\]
In this case, Nature takes the Nth root.
A semiquantitative perspective
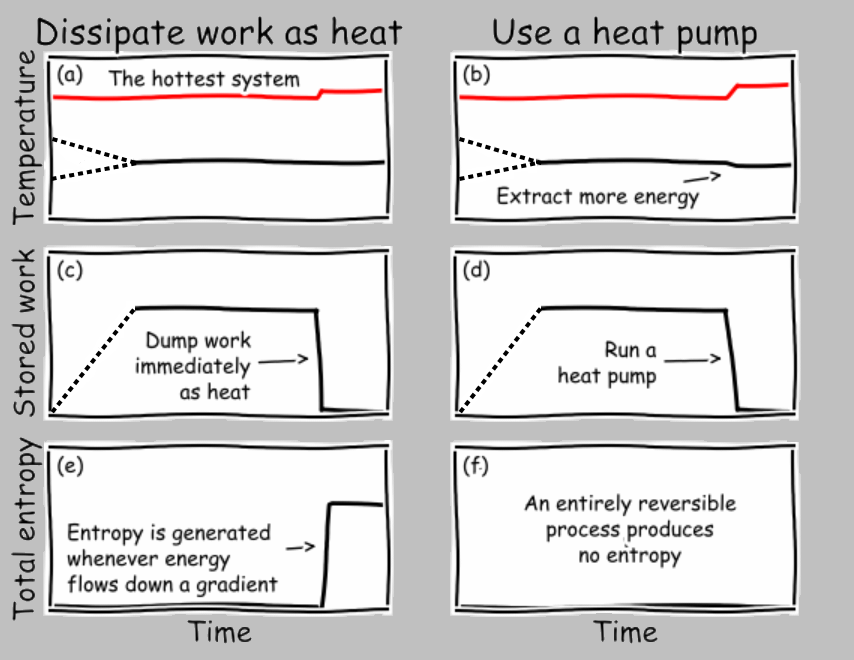
Let’s plot the temperature, extracted work, and entropy generation of the two conditions of the systems pushed together vs. the systems connected by a heat engine. And to gain insight concerning the idea of reaching equivalent states, let’s imagine that after we extract the maximum amount of work in the heat-engine case, we simply dump that energy back into the two systems (by, say, dissipating electrical current through a resistor, or bringing a spinning wheel to a halt through friction, or letting a suspended weight fall to the ground):
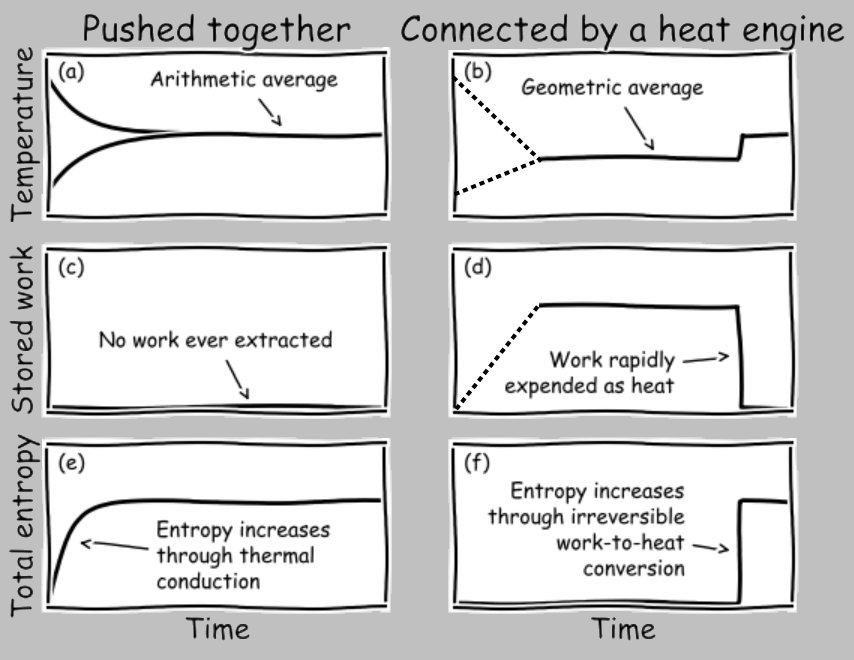
Let’s take these subfigures one at a time. In (a), we push the two systems into thermal contact, where they exchange energy (through conduction, for example). It’s generally the case that the heat flux depends on the temperature difference, and the resulting differential equation tells us that the temperatures exponentially converge toward the final arithmetic average.
In (b), we can imagine our idealized Carnot engine extracting energy from the temperature difference at, say, a constant rate (in a real engine, the power output would likely decrease as the temperature difference is eliminated, and the Carnot cycle must run infinitesimally slowly in any case, so let’s just connect the initial and final states with a dashed line) and shunting some entropy (in the form of heat transfer) to the cold reservoir as discussed earlier. Soon after the engine completes its operation, we dump all the extracted work into the joint system. The temperature rapidly rises to the arithmetic average shown in (a).
In (c), no work is extracted when two systems are pushed together in thermal contact. Simple enough.
In (d), the extracted work accumulates as the engine operates. Later, this stored energy is depleted by heating the two systems equally.
In (e), entropy is rapidly generated as energy moves down a (continuously decreasing) thermal gradient.
In (f), the operation of the reversible engine produces no entropy; the only entropy generation occurs when the extracted work is converted irreversibly into thermal energy.
The important insight to obtain from these charts is that the exact same state is obtained by (1) smushing the systems together or (2) extracting energy through work and then dissipating this work as thermal energy. This finding satisfies our expectation that any two identical environments (here, a pair of systems) brought to the same state should exhibit matching state variables, including their temperature and entropy. In contrast, the amounts of transferred work and heat differ between the two scenarios, which is fine, as work and heat are not state variables.
A final twist: The three-system case
If the above findings seem straightforward, consider another example: if we had not two but three identical systems, we could connect two by a heat engine and use the extracted energy to heat the third. What’s the maximum temperature we can achieve in one of the systems for three systems at initial arbitrary absolute temperatures \(T_1\), \(T_2\), and \(T_3\)?

Three identical systems: what’s the hottest we can make one system at the expense of cooling the other two?
As before, we’d like to connect a heat engine between two of the three systems; the novel step is to use the obtained energy to make the third system as hot as possible. This example is adapted from Callen’s Thermodynamics and an Introduction to Thermostatistics (Wiley 1985). Before showing the solution strategy, a couple of hints:
Hint 1: At the end of the process, the two cooler systems must be at the same temperature; otherwise, we could continue operating a heat engine between them to make the third system hotter.
Hint 2: The optimal solution is not to dump the extracted work into the third system in the form of heat (!).
The solution is as follows: Let the two cooler systems ultimately obtain a temperature of \(T_\mathrm{cooler}\), and let the hotter system ultimately obtain a temperature of \(T_\mathrm{hotter}\). By conservation of energy, we have
\[T_\mathrm{hotter}+2T_\mathrm{cooler}=T_1+T_2+T_3.\]
Without loss of generality, we can assume that system 3 ultimately ends up the hottest; then, we can integrate the entropy changes as follows:
\[\Delta S=C\ln\left(\frac{T_\mathrm{cooler}}{T_1}\right)+C\ln\left(\frac{T_\mathrm{cooler}}{T_2}\right)+C\ln\left(\frac{T_\mathrm{hotter}}{T_3}\right);\]
\[\Delta S = C\ln\Bigg(\frac{ T_\mathrm{hotter} T_\mathrm{cooler}^{2} }{T_1 T_2 T_3}\Bigg).\]
(It’s straightforward to show that we obtain this result no matter which system is ultimately the hottest one.)
The paraconservation of entropy tells us that the total entropy change must be positive or zero, so \( \Delta S \ge 0 \), which gives us
\[T_\mathrm{hotter}T_\mathrm{cooler}^2\ge T_1T_2T_3.\]
Plugging the energy conservation equation into this equation, we obtain
\[(T_1+T_2+T_3-T_\mathrm{hotter})^2T_\mathrm{hotter}\ge 4T_1T_2T_3\;\mathrm{(inequality\;1)}.\]
And since we can’t cool anything to 0 K or below, we must also satisfy
\[T_\mathrm{cooler}=\frac{T_1+T_2+T_3-T_\mathrm{hotter}}{2}\gt 0,\]
or
\[T_\mathrm{hotter}\lt T_1+T_2+T_3\;\mathrm{(inequality\;2)}.\]
It’s not particularly useful to solve the cubic-order inequality 1; it’s more instructive to look at the solution graphically, as Callen does. Consider the initial temperatures of \(T_1=100\;K\), \(T_2=200\;K\), and \(T_3=300\;K\). Shown below are the two inequalities marked on a plot of \((T_1+T_2+T_3-T_\mathrm{hotter})^2T_\mathrm{hotter}\) vs. \(T_\mathrm{hotter}\):
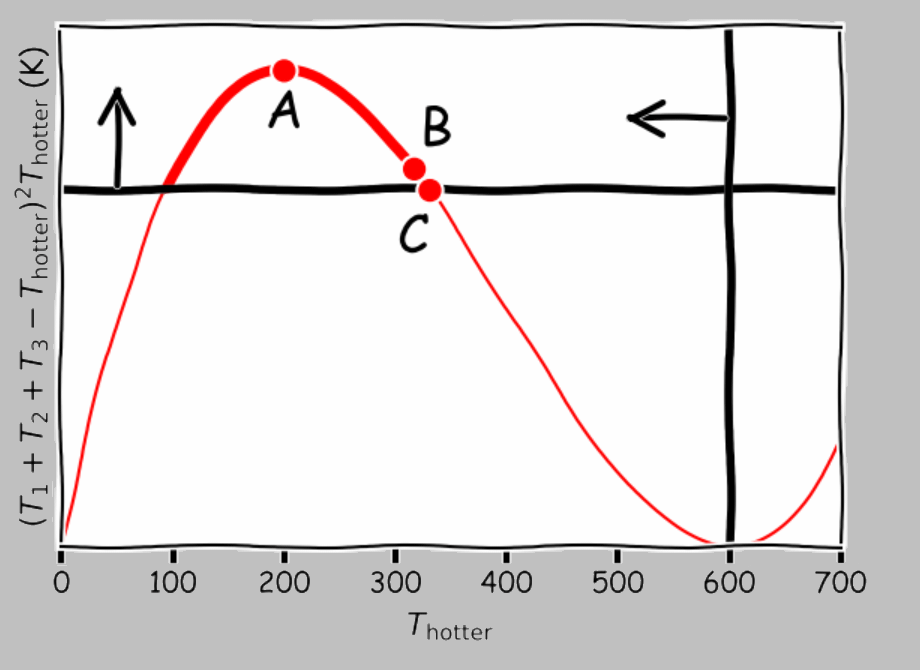
Line of possibilities (thick red segment) for changing the temperature of a single system within a trinary system with \(T_1=100\;\mathrm{K}\), \(T_2=200\;\mathrm{K}\), and \(T_3=300\;\mathrm{K}\). Point A corresponds to bringing the systems together into thermal contact; point B exploits the temperature difference between the two cooler systems to heat the third by resistive heating or some other completely irreversible process. Point C, the optimal solution, uses the extracted energy from the two cooler systems to pull out even more energy.
The thicker part of the red line shows the possibilities allowed by the constraints of energy conservation and the two inequalities, representing paraconservation of entropy and positive temperature. The peak of the curve (point A, which represents the maximum production of entropy) corresponds to pushing all three systems together to obtain a final temperature of 200°C. Farther to the right, at point B (317°C), we have the now-familiar approach of extracting work from a temperature difference and dumping the heat directly:

Dumping heat-engine-extracted work into the third system is one way to heat it; surprisingly, however, this approach doesn’t maximize its temperature.
Notably, however, we could do better. If we used a reversible heat pump to move additional thermal energy from \(T_1\) and \(T_2\) to cool them even further, we could obtain an even higher temperature in \(T_3\) (point C, 331°C) and produce no entropy at all during the entire process:

A reversible heat pump can be used to extract additional thermal energy from the first two systems even after the temperature difference between them is eliminated.
Conceptually, this approach is no different from running a (highly efficient) refrigerator. After all, a refrigerator uses electrical work to remove thermal energy from already-cool food and transfer it to your kitchen. Alternatively, consider heating your home either by (1) a electronic heating element (or a overclocked computer, for example) or (2) a heat pump. Strategy (1) is guaranteed to turn every bit of work into heat; however, impressively, strategy (2) can use one unit of work to transfer multiple units of thermal energy.
Shown below are the two strategies shown in terms of the individual system temperature, extracted work, and total entropy. Note that this time, the two examples don’t end up in the same state; using a heat pump, we attain a greater final difference between the hotter system and the two cooler ones, as we hoped to accomplish.
|