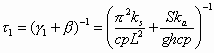The transient response of the V-beam thermal actuators can be predicted by examining the time-dependent form of Equation (4):
(26)
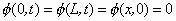
where the values of the specific heat c and density p of silicon are assumed to be independent of temperature, and the following variable substitutions have been made:
(27)
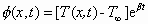
(28)
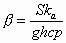
Applying the finite Fourier transform to Equation (25) results in the following nonhomogeneous differential equation:
where
(30)
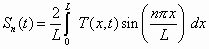
(31)
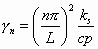
(32)
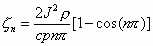
Equation (29) has the solution
(33)
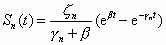
to which the inverse finite Fourier transform can be applied:
(34)
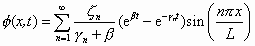
The general solution is therefore
(35)
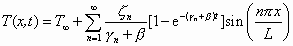
implying a first-mode time constant of
which offers a useful way of comparing heat loss contributions from beam conduction and air conduction. The first term represents heat loss through the beam to the anchors; the second term represents heat loss through the air gap to the substrate. By using the values in Table 3, a typical V-beam actuator with a length L of 1000 mm, a width w of 10 mm, and a height h of 50 mm is predicted to have a first-mode time constant t1 of approximately 0.8 ms. The corresponding cut-off frequency is approximately 200 Hz. This frequency is low compared to polysilicon equivalents because of the larger thermal mass of the high-aspect-ratio V-beam actuators [41].
The dynamic response of the V-beam actuators at or near the mechanical resonance frequency is not expected to affect actuator operation, as this frequency is much larger than the thermal cut-off frequency. The natural frequency of the first mode of vibration of a clamped-clamped beam can be calculated using the following equation [adapted from 45]:
(37)
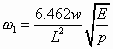
By approximating a V-beam actuator as a clamped-clamped beam and applying the same dimensions as those given above, the first-mode natural frequency is estimated to be 87 kHz.